Summary

Agents that threaten to harm other agents, either in an attempt at extortion or as part of a conflict, are an important form of agential s-risks because the execution of such threats could cause large amounts of disvalue.

This post is an attempt to isolate heuristics that determine when such threats are attractive, which is valuable because it improves our general understanding of threats and allows us to derive corresponding anti-extortion strategies.

The key takeaway is that extortion only works well if all of the following three (heuristic) conditions are fulfilled to a sufficient extent:

The ratio of how much the threatener can gain vs. how much he can lose is high.
The ratio of how much the threatenee can gain or lose relative to giving in is low.
The threat reduces the utility of the threatenee (much) more than the utility of the threatener.

Contents

1 Technical framework
2 Anti-extortion strategies
3 Further research questions

Technical framework

As a simple example of extortion, suppose Alice and Bob each own USD 10,000 and have a utility function that’s linear with respect to money. Alice has a button that would destroy all of Bob’s money at a cost of USD 500 for herself. She threatens to press that button unless Bob sends her USD 1000.

I will use the following notation:

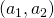$(a_1,a_2)$ for the resulting utilities of the threatener (index 1) and threatenee (index 2) if the threat is successful, i.e. the threatenee gives in
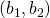$(b_1,b_2)$ are the results for threatener and threatenee if nothing happens, i.e. no threat is made or the threatenee does not give in and the threat is not carried out.
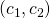$(c_1,c_2)$ if the threatenee does not give in and the threatener still carries through with the threat.

We can usually expect $a_1 > b_1 > c_1$ and $b_2 > a_2 > c_2$ . In the above example, we get $a_1 = 11000, b_1 = 10000, c_1 = 9500, b_2 = 10000, a_2 = 9000, c_2 = 0.$

How much can the threatener gain or lose?

It seems intuitively clear that extortion is more plausible if the threatener can gain a lot from it or if the cost of going through with the threat is negligible.

Compared to the default outcome of not making threats, which yields a utility of $b_1$ , the threatener can gain an additional utility of $a_1 - b_1$ if his attempt at extortion is successful (resulting in $a_1$ instead of $b_1$ ). The potential loss is $b_1 - c_1$ .

Since utility functions are defined only up to positive affine transformations, we can set $b_1 = 0 = b_2 = 0$ without loss of generality. If we normalize the utilities in this way, then the potential gain and loss is $a_1$ and $-c_1$ .

Given this, we can define the ratio

$r_1 = -\frac{a_1-b_1}{b_1-c_1} = -\frac{a_1}{c_1}$

as a measure for how much the threatener can gain or lose. Since $a_1 > b_1 = 0 > c_1$ , the ratio $r_1$ is always positive.

All else equal, threats arguably work better (for the extortionist) if $r_1$ is high, and don’t work well if $r_1$ is small. For example, the attempt at extortion is much less plausible if Alice’s button destroys USD 5000 of her own money ( $r_1 = 0.2$ ) rather than USD 500 ( $r_1 = 2$ ).

How much can the threatenee gain or lose?

Not being threatened at all (yielding utility $b_2$ ) is the best possible outcome for the threatenee, so she can only lose – that’s the catch of extortion. The relevant question is how much the threatenee can gain or lose by refusing to give in, relative to the outcome where she just pays up.

The ratio

$r_2 = \frac{b_2 - a_2}{a_2 - c_2} = \frac{a_2}{c_2 - a_2}$

is a measure of this. Since $b_2 = 0 > a_2 > c_2$ , this ratio is also always positive.

If $r_2$ is close to 0, then the execution of the threat is many times worse for the threatenee than giving in, which means that extortion works better (relatively speaking). If Alice demands only USD 10 ( $r_2 = 0.001$ ), Bob might be willing to pay because the loss is negligible compared to the danger of losing his entire USD 10000. Conversely, demanding USD 9000 ( $r_2 = 9$ ) would be unreasonable because it’s almost as bad as the threat itself, in which case Bob is incentivized to not give in.

How costly is the threat?

A third interesting factor is the “threat ratio”

$t = \frac{b_2 - c_2}{b_1 - c_1} = \frac{c_2}{c_1}.$

It measures how much the threat harms the threatenee compared to its cost to the threatener in terms of normalized utility.

To see that this is an important measure, consider what would happen if Alice’s button destroyed all of her own money ( $t = 1$ ) rather than USD 500 as in the original formulation ( $t = 20$ ). In that case, the threat lacks credibility because it would harm Alice just as much as it harms Bob. It is intuitively plausible that extortion probably does not work in such a situation, even though there seems to be no fundamental obstacle.

Feasibility of extortion

Extortion is more attractive, and the threatenee is more vulnerable, if $r_1$ is high, $r_2$ is small, and $t$ is high. Heuristically, I would expect that extortion only works well if $r_1 > 1$ , $r_2 < 1$ , and $t > 1$ .

Interestingly, it seems that all three parameters have to be favorable. In other words, extortion becomes infeasible if only one of the factors favors the threatenee.

For example, if strong counterthreats are available, then $r_1$ is significantly lower because the threatener has more to lose. This makes extortion much less attractive even if the other parameters are favorable ( $r_2$ is low and $t$ is high). A real-world example is mutual deterrence in the cold war: since both sides can harm the other, it would not make much sense to say “give us money or we drop a nuclear bomb on you”. In this setting, the threat ratio t is large and $r_2$ is small (both favoring the threat), but $r_1$ is also small, making the threat unattractive.

(See above for examples that don’t work well because of $r_2$ or $t$ .)

Anti-extortion strategies

To the extent this framework is useful for judging whether extortion is possible in a given situation, it is also useful for thinking about anti-extortion strategies. We should find ways to systematically change each of the parameters so that extortion becomes less attractive (i.e. decrease $r_1$ and $t$ , increase $r_2$ ).

For example, building a coalition against extortionists and punishing any attempt at making (illegitimate) threats helps because it decreases $r_1$ . Our contemporary society implements this anti-extortion strategy by simply making extortion a criminal offense, which seems to work reasonably well in practice given the level of risk-aversion of most people.

Another interesting (but perhaps not very practical) strategy is to only build up resources that are less useful to potential extortionists. This also decreases $r_1$ . For example, knowledge about the world or educational degrees can, unlike money, not be transferred to another person (or at least not as easily). If Bob had a PhD instead of money, and Alice had a button that annuls his PhD and erases any memory of it, she still couldn’t extort him because he doesn’t have anything that Alice wants.

Similarly, we could come up with ways to alter the other parameters. For instance, successfully misrepresenting or hiding your values would decrease both $r_2$ and $t$ because the threatener is unable to find the most effective threat.

Reducing the divergence in values across different agents is a potentially promising strategy to reduce the threat ratio t. If most people share a lot of common values, it’s more likely that any particular threat would also harm the extortionist, making it much less attractive.

Further research questions

Needless to say, this post is only a small first step towards understanding when extortion works and how we can prevent it. Much more research is necessary to obtain the necessary theoretical and practical tools to analyse how extortion works.

I suggest looking into the following related questions:

What if the threatener can choose the size of her threat and demands freely? This means that the threatener has some degree of control over the value 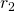$r_2$ . A big threat size or asking for a small amount of resources lead to a small 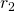$r_2$ , while the converse would make it large. But the threat ratio t remains the same, and a bigger threat also reduces 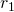$r_1$ since it is more costly. So the threatener can optimize the parameters, but there are tradeoffs and she wouldn’t necessarily end up choosing arbitrarily big threat sizes. I find this fairly intuitive, but it would be valuable to have a better formal account of how extortionists would choose threat sizes.
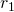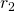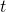Since $r_1$ , $r_2$ and $t$ are still fairly abstract, one could ask what factors affect the values of these ratios in practice, or analyse what the values are in real-world examples.
In this post, I assume (for simplicity) that the relevant agents are a single extortionist and the threatenee. But what happens in a multi-agent situation, with many potential threateners and threatenees who have different utility functions?
The credibility of threats is often a key factor. How does this fit into the framework of this post? Intuitively, it seems clear that threats are more or less credible depending on the payoff structure, but what does that mean more precisely?

Heuristics to assess the feasibility of threats